Casse-tête

Solutions aux casse-tête du dernier numéro

Question 1

1. Nous n'essayerons pas de retracer ici l'histoire de la Lune depuis sa formation; d'ailleurs qui pourrait la relater avec certitude? En supposant toutefois que la Lune s'est retrouvée un jour à tourner sur elle-même en un temps voisin d'un mois, il est alors relativement simple de comprendre pourquoi elle a été amenée à nous présenter toujours la même face, étant donné sa forme allongée. En effet, si sa période de rotation sur elle-même était légèrement différente d'un mois, son axe long viendrait à ne plus être aligné sur la Terre et cette dernière exercerait alors un couple de force sur la Lune, qui tendrait à ramener son axe long vers la Terre et par le fait même à synchroniser sa période de rotation sur elle-même à la durée d'un mois. Ce couple de force existe en raison de la décroissance de l'attraction terrestre en fonction de la distance, ce qui cause une force de marée sur la Lune (cette force de marée est en fait la dérivée par rapport à la distance de la force de gravitation terrestre). Cette même force de marée qui produit un couple stabilisateur sur la Lune est aussi à l'origine de sa forme allongée vers la Terre. Ainsi donc, cette force de marée rend la situation présente stable. Il n'en serait peut-être pas ainsi si la Lune était plus éloignée, car cette force diminue comme le cube de la distance.

Question 2

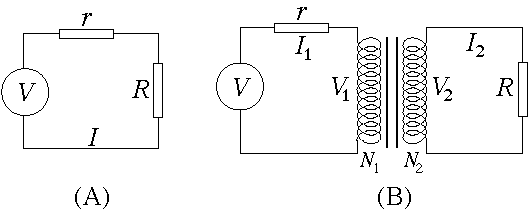
2. Supposons, dans un modèle extrêmement naïf, qu'on puisse considérer la ligne de transmission comme une résistance r et la charge du réseau (c'est-à-dire l'ensemble des clients d'Hydro-Québec) comme une résistance R. Supposons de plus que les deux résistances sont placées en série, comme illustré en (A) ci-haut. Dans ce cas, la puissance dissipée dans la ligne est rI² et celle transmise au réseau est RI², de sorte que le rapport des pertes à la charge utile est r/R, indépendamment de la tension utilisée. D'après cette analyse, il n'y a pas d'avantage à élever la tension du réseau. Cependant, cet argument est erroné, car la charge du réseau et la ligne de transmission ne sont pas sur un même circuit : il y a une série de transformateurs entre les deux. Dans un autre modèle très naïf (mais moins que le premier), on représente le réseau comme illustré en (B) : le circuit primaire (portant un courant I₁) est celui de la ligne de transmission, alimentée par une tension V. Le circuit secondaire est celui de la charge du réseau, qui porte un courant I₂. Les deux circuits sont couplés par un transformateur comportant N₁ tours du côté primaire et N₂ du côté secondaire. Les tensions aux bornes du transformateur de chaque côté sont respectivement V₁ et V₂. On peut montrer -- l'espace nous manque ici pour le faire -- que le rapport des tensions est V₁/V₂=N₁/N₂ et que le rapport des courants est (approximativement) l'inverse, soit I₁/I₂=N₂/N₁, de sorte que V₁I₁ = V₂I₂. Donc le rapport des pertes à la charge utile est maintenant rI₁²/RI₂² = (r/R)(N₂/N₁)². Par exemple, en choisissant N₁/N₂=100, on réduit ce rapport de 10 000 en comparaison avec un circuit simple. Là est essentiellement l'avantage d'augmenter la tension dans les lignes de transmission. Notez que la tension produite par la centrale électrique a aussi besoin d'être augmentée à l'aide de transformateurs avant de nourrir la ligne de transmission. Un dernier commentaire : le modèle présenté ci-dessus est une caricature grossière de la réalité. Un réseau de transmission et de distribution ne peut être décrit correctement par des résistances seulement, ses éléments ne peuvent pas être décrits non plus de manière localisée (comme les éléments d'un circuit de laboratoire) et le grand nombre de stations, de niveaux de tension, etc. rend les choses assez complexes. Mais l'idée de base est la même que celle expliquée ici.

Nouveaux casse-tête

1. Fixons une petite chandelle dans un bocal, allumons-là et fermons le couvercle hermétiquement. La chandelle brûle un certain temps et puis s'éteint, par manque d'oxygène. Maintenant, juste après avoir fermé le couvercle, laissons tomber le bocal en chute libre. On observe que la chandelle s'éteint tout de suite (lors de la chute). Qu'est-ce qui cause cette extinction subite? Comme le bocal est bien fermé, le flot de l'air autour du bocal ne devrait pas influencer la chandelle!

2. La Lune tourne autour de la Terre et la Terre autour du Soleil, approximativement en suivant une trajectoire circulaire. Quelle doit être alors le type de trajectoire suivi par la lune, vu d'un observateur au repos par rapport au Soleil? Lequel des trois choix ci-dessous correspond le mieux à la réalité et pourquoi? Notez que l'orbite (B) comporte des portions concaves, alors que l'orbite (C) n'en contient pas.

Mise en page par Gilbert Vachon

revue@physique.usherb.ca