 revue@physique.usherb.ca
revue@physique.usherb.ca
| L'Attracteur No. 10 Automne 2000 | LA REVUE DE PHYSIQUE | ISSN 1207-0203 |
Casse-tête
Solutions aux casse-tête du dernier numéro
Question 1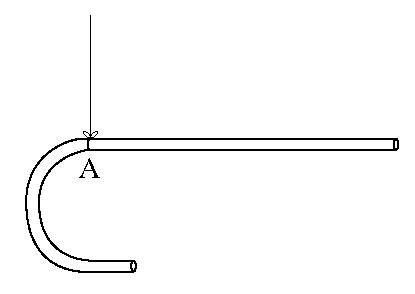 1. Zig a tort. Si un objet rigide est en équilibre, suspendu par un fil,
cela signifie que le centre de masse de l'objet est sur la droite qui prolonge le fil.
Cependant, rien ne garantit qu'il y ait autant de masse à droite qu'à gauche du centre
de masse, à moins que l'objet ait une symétrie évidente, ce qui n'est pas le cas ici.
En réalité, il y aura plus de masse dans la moitié de gauche (voir la figure ci-contre), car elle
s'étend moins loin du point de suspension que la moitié droite. Le principe de base ici e
st que le couple de force, causé par la gravité et agissant sur la canne par rapport au point
de suspension, doit être nul, afin que la canne soit en équilibre de rotation. La moitié droite
de la canne ayant un levier plus long en moyenne que la moitié gauche, elle n'a pas besoin d'être
aussi massive que la gauche pour subir un couple exactement opposé à celui de l'autre moitié.
1. Zig a tort. Si un objet rigide est en équilibre, suspendu par un fil,
cela signifie que le centre de masse de l'objet est sur la droite qui prolonge le fil.
Cependant, rien ne garantit qu'il y ait autant de masse à droite qu'à gauche du centre
de masse, à moins que l'objet ait une symétrie évidente, ce qui n'est pas le cas ici.
En réalité, il y aura plus de masse dans la moitié de gauche (voir la figure ci-contre), car elle
s'étend moins loin du point de suspension que la moitié droite. Le principe de base ici e
st que le couple de force, causé par la gravité et agissant sur la canne par rapport au point
de suspension, doit être nul, afin que la canne soit en équilibre de rotation. La moitié droite
de la canne ayant un levier plus long en moyenne que la moitié gauche, elle n'a pas besoin d'être
aussi massive que la gauche pour subir un couple exactement opposé à celui de l'autre moitié.
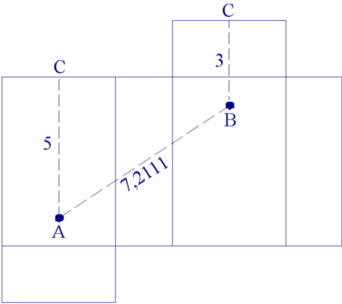 2. Le chemin le plus court entre deux points d'un espace plat est une ligne droite.
La boîte est effectivement un espace plat, si on la déplie comme illustré. Plus précisément,
la courbure de la boîte est concentrée sur les coins, en une singularité mathématique,
alors que les arêtes, qui peuvent être dépliées, ne portent aucune courbure. Il suffit
alors de relier les points A et B par une droite directe, qui est oblique par rapport aux
faces et qui mesure
2. Le chemin le plus court entre deux points d'un espace plat est une ligne droite.
La boîte est effectivement un espace plat, si on la déplie comme illustré. Plus précisément,
la courbure de la boîte est concentrée sur les coins, en une singularité mathématique,
alors que les arêtes, qui peuvent être dépliées, ne portent aucune courbure. Il suffit
alors de relier les points A et B par une droite directe, qui est oblique par rapport aux
faces et qui mesure
Mise en page par Gilbert Vachon